Zkouška Töpfer 26.1.2026
1. (10 bodů)
Na vstupu je dán AVL strom (tj. výškově vyvážený binární vyhledávací strom), v jehož vrcholech jsou uložena celá čísla
a celá čísla d a h taková, že d ≤ h.
Určete nejmenší prvek a největší prvek ve vstupním stromu, které leží v uzavřeném intervalu ⟨d, h⟩.
Pokud žádný takový neexistuje, na výstupu bude hodnota None.
Pozor na to, že čísla d a h se ve stromu vůbec nemusí vyskytovat.
Navrhněte postup, jak správně vyřešit úlohu s co nejlepší časovou a prostorovou složitostí (měřeno nejhorším případem) vzhledem k počtu vrcholů AVL stromu.
(a) Popište algoritmus (včetně datových struktur, které případně budete používat). Programový kód není povinný, slovní vysvětlení zvoleného postupu řešení naopak povinné je.
Nepoužívejte prosím žádné netriviální datové struktury (jako jsou např. datové typy dictionary či set v jazyce Python), jejichž algoritmus sami nepopíšete a neodvodíte jeho časovou složitost.
(b) Zdůvodněte správnost algoritmu.
(c) Odvoďte časovou a prostorovou složitost (v nejhorším případě).
Příklad:
vstup: 7 70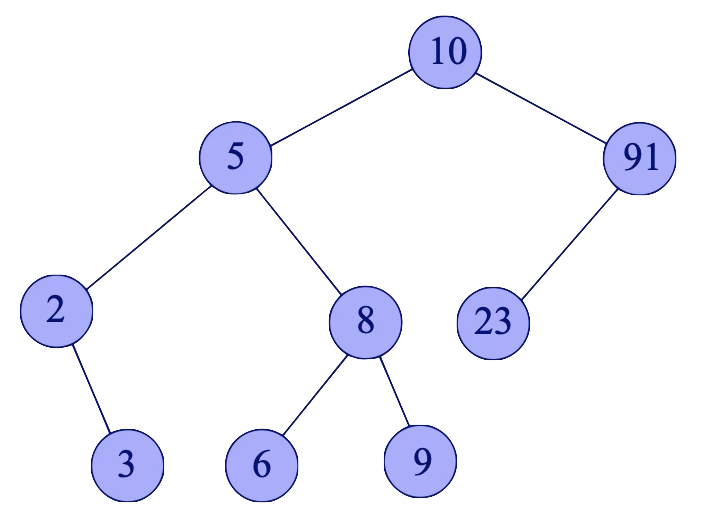
výstup: 8 23
Poznámka: Za jednoduché řešení s časovou složitostí Θ(n) bude udělen jen nízký počet bodů.
2. (10 bodů)
Na vstupu jsou zadány dva lineární spojové seznamy uspořádané tak, že hodnoty jejich uzlů tvoří rostoucí posloupnosti.
V jednom seznamu tedy nemohou být různé uzly se stejnými hodnotami. Stejné hodnoty se ovšem mohou vyskytovat v různých seznamech a právě o ty nám jde.
Sestavte funkci v jazyce Python, která vrátí spojový seznam tvořený uzly s hodnotami, které se vyskytují současně v prvním i ve druhém seznamu.
Hodnoty uzlů výstupního seznamu budou opět uspořádány vzestupně.
Seznamy nevytvářejte ze vstupních dat ani je nevypisujte, funkce pouze upraví již existující seznamy podle požadavků zadání.
Funkce nebude alokovat nové uzly, výsledný seznam postaví z uzlů původních seznamů.
Nezapomeňte ošetřit všechny zvláštní případy: prázdný seznam, jednoprvkový seznam apod.
Navržená funkce nesmí používat žádná pole (tj. datový typ
listv Pythonu).
(a) Svoje řešení zapište jako funkci v Pythonu, využijte k tomu definici třídy pro uzel spojového seznamu i hlavičku funkce uvedené níže a váš kód prosím opatřete komentáři,
(b) zdůvodněte správnost,
(c) odvoďte časovou složitost (metodou nejhoršího případu).
class Uzel:
"""trida pro reprezentaci uzlu spojoveho seznamu"""
def __init__(self, hodnota = None, dalsi = None):
self.hodnota = hodnota # hodnota ulozena v uzlu
self.dalsi = dalsi # odkaz na dalsi uzel
def prunik(prvni: Uzel, druhy: Uzel) -> Uzel:
"""
prvni, druhy : odkazy na zacatky vstupních spojovych seznamu
vrátí : spojovy seznam s prvky, ktere lezi v obou seznamech
"""
Příklad:
Vstup  Výstup
Výstup 
3.
Odpovězte na otázky, své odpovědi vždy zdůvodněte. Všechny časové složitosti uvedené níže měří složitost metodou nejhoršího případu.
(a) (5 bodů)
Vstup:
binární max-halda o n prvcích, uložená v poli
a(kořen haldy je uložen va[0])index
i
Výstup:
max-halda, v níž byl prvek a[i] odstraněn, hodnoty ostatních prvků jsou stejné, je uložena ve stejném poli a, jen počet prvků bude nyní samozřejmě n-1.
Poznámka: Operace odstranění prvku může vyvolat nutnost změnit pořadí zbylých prvků v poli a tak, aby upravené pole opět představovalo max-haldu.
Dokažte nebo vyvraťte následující tvrzení, svoji odpověď zdůvodněte:
Existuje algoritmus, který problém vyřeší v čase Θ(log n).
(b) (5 bodů)
Na vstupu je dáno vzestupně setříděné pole a délky n a hodnoty x a y takové, že x ≤ y.
Naším cílem je nalézt (libovolný) index i takový, že x ≤ a[i] ≤ y. Pokud žádný takový neexistuje, vrátíme hodnotu None.
Profesor Hammerstein se na přednášce otázal studentů, co lze říci o časové složitosti řešení uvedeného problému porovnávacím algoritmem.
(Porovnávací algoritmus přistupuje k prvkům zadaným na vstupu prostřednictvím operace porovnání dvou prvků p < q, p > q, p ≤ q, p ≥ q, p = q, hodnoty prvků jinak nevyužívá.)
Steve se domnívá, že existuje porovnávací algoritmus, který vyřeší problém v čase O(log n);
Bill soudí, že každý porovnávací algoritmus řešení problému má časovou složitost třídy Ω(log n).
Kteří studenti mají pravdu a kteří nikoliv?
(Steve – ANO / NE, Bill – ANO / NE)
Svoji odpověď zdůvodněte!