Zkouška Töpfer 12.1.2026

1. (10 bodů) Na vstupu jsou zadána dvě pole a a b, jejichž prvky

jsou čísla (ne nutně celá),
nejsou nijak uspořádány,
ovšem mohou se libovolně opakovat.

Sestrojte pole c, které bude obsahovat právě ty prvky,

které se buďto v a vyskytují vícekrát než v b
nebo se v b vyskytují vícekrát než v a
přičemž počet výskytů každého takového prvku ve výsledném poli c je roven absolutní hodnotě rozdílu počtu jeho výskytů v polích a a b.

Navrhněte postup, jak správně vyřešit úlohu s co nejlepší časovou a prostorovou složitostí (měřeno nejhorším případem) vzhledem k délce vstupních polí.

(a) Popište algoritmus (včetně datových struktur, které případně budete používat). Programový kód není povinný, slovní vysvětlení zvoleného postupu řešení naopak povinné je. Nepoužívejte prosím žádné netriviální datové struktury (jako jsou např. datové typy dictionary či set v jazyce Python), jejichž algoritmus sami nepopíšete a neodvodíte jeho časovou složitost.

(b) Zdůvodněte správnost algoritmu.

Příklad: vstup: [2,8,5,8,0,0,7,2,0,20] [10,8,20,0,2,2,10,7]

výstup: [10,10,8,5,0,0]

Poznámka: Pořadí na výstupu může být zcela libovolné, tedy i jiné než v uvedeném příkladě.

Klikni pro studentské řešení (spoiler)

Není to zdůvodnění jak chce a), b), c), ale přesto může pomoct :) Je to řešení bez dictionary nebo set, jak chce zadání, se složitostí $O(n \cdot \log(n))$ . Je to komentované víc, než je možná třeba, ale je to tak schválně - komentáře třeba pomohou některým k snažšímu pochopení. Ti, komu se zdají nadbytečné - prosím neodstraňujte, buďte shovívaví. Je jednodušší při učení si materiál zestručnit, když mu rozumíte, než zobsáhlit, když ne :)

a = [2,8,5,8,0,0,7,2,0,20]
b = [10,8,20,0,2,2,10,7]
a.sort()
b.sort()

def reseni(a,b):
    c = []
    i = 0
    j = 0
    # dokud je ty jezdce kam posouvat
    while i != len(a) - 1 or j != len(b) - 1:
        # porovnani poctu stejnych prvku
        if a[i] == b[j]:
            pocet_a = 0
            pocet_b = 0
            prvek = a[i]
            # po tomhle budou i,j ukazovat na nejblizsi prvky za tim, na ty, co se uz lisi
            while a[i] == prvek:
                pocet_a += 1
                i += 1
            while b[j] == prvek:
                pocet_b += 1
                j += 1
            # a kdyz uz to mame spoctene, tak pridani tolikrat, co nam rika zadani
            for _ in range(abs(pocet_a - pocet_b)):
                c.append(prvek)
        else:
            # muzeme udelat diky tomu, ze mame oba seznamy serazene
            # proste prvky co jsou jenom v jednom seznamu vypiseme a pricitame ten index
            # pokud takovych prvku bude vic, tak se v dalsi iteraci while sem dostaneme znova
            # a to az do chvile, co se ty prvky zase nezacnou shodovat 
            # (coz pokud prvky spolecne seznamum a,b jeste jsou, tak musi znovu nastat diky razeni, zadne prvky nezapomeneme)
            if a[i] < b[j]:
                c.append(a[i])
                i += 1
            elif b[j] < a[i]:
                c.append(b[j])
                j += 1
    print(c)

reseni(a,b)

2. (10 bodů) Je zadán strom logického výrazu,

tj. binární strom, v jehož vnitřních vrcholech jsou uloženy operátory and, or či not (jako hodnoty typu string)
a v listech logické hodnoty True, False (tj. hodnoty typu bool),

a logická hodnota h (která nabývá hodnoty True či False). Navrhněte efektivní algoritmus, který vrátí

maximální výšku podstromu, který reprezentuje podvýraz o zadané hodnotě h
nebo hodnotu None, pokud žádný takový podstrom neexistuje.

Podstrom reprezentující podvýraz je jednoznačně určen svým kořenem, obsahuje tedy všechny následníky kořene z původního stromu a hrany do nich vedoucí. Vrchol stromu, v němž je uložen operátor not, má vždy jediné dítě; můžeme předpokládat, že vždy půjde o levé dítě.

(a) Svoje řešení zapište jako funkci v Pythonu, využijte k tomu definici třídy pro vrchol binárního stromu i hlavičku funkce uvedené níže a váš kód prosím opatřete komentáři,

(b) zdůvodněte správnost,

class VrcholBinStromu:

   """třída pro reprezentaci vrcholu binárního stromu"""  
   def  __init__(self, data =  None, levy =  None, pravy =  None):
      self.levy = levy    # levé dítě  
      self.pravy = pravy  # pravé dítě
      self.data = data    # hodnoty (operátory či operandy) uložené ve vrcholech 
  

def vyska(koren: VrcholBinStromu, h: bool):

    """
    koren : kořen zadaného binárního stromu
    h     : True či False
    vrátí : maximální výšku podstromu reprezentujícího podvýraz, který se vyhodnotí na hodnotu h
    """

Poznámka: Definici třídy ani hlavičku funkce prosím neměňte, můžete si ovšem definovat vlastní pomocnou funkci (funkce) dle potřeby.

Příklad: vstup:

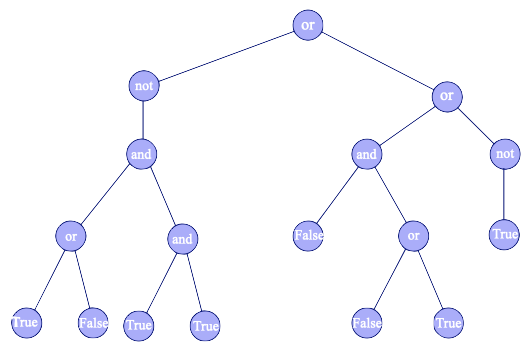strom logického výrazu , True

(opravdu to tak bylo zadané, v této grafické podobě. Obrázek stromu a vedle hodnota, na kterou se ten hledaný podstrom má vyhodnotit, tedy True)

výstup: 2

zdůvodnění: Podstrom zakořeněný v nejlevějším vnoučeti kořene má výšku 2 a reprezentuje podvýraz o hodnotě True. Naopak žádný podstrom reprezentující podvýraz o hodnotě True o výšce alespoň 3 ve stromě není.

Spoiler: jak na to

Kód si napište, spíš jen nápověda. 1 z možných způsobů je:

Vyhodnotit celý strom a výsledky si ukládat ke každému vrcholu. Tak, aby každý vrchol v sobě měl výsledek jeho podstromu, a výšku svého podstromu (max(levý podstrom, pravý podstrom) + 1). To se hezky píše rekurzivně.
Pak si strom se spočtenými hodnotami projít ještě jednou a podívat se, u každého vrcholu, jestli vrchol má výsledek co chci, a jestli ano, tak se podívat na hloubku jeho podstromu. Budu si pamatovat nejvyšší zatím nalezenou hloubku podstromu, a až projdu celý strom, tak určitě najdu ten nejvyšší podstrom, co se vyhodnotí na hledanou hodnotu.

Dva průchody stromem, kde provádím O(1) operace na každý vrchol, mají časovou složitost lineární k počtu vrcholů stromu.

(Krok 2. jde sloučit s krokem 1., kdy se rovnou, když dostanu výsledek, budu dívat na to, jestli to je ten hledaný výsledek, a jestli je hloubka vyšší než nejvyšší zatím nalezená. Ale to už je docela jedno, složitost neovlivní.)

3. Odpovězte na otázky..

(a) (5 bodů) Prvek posloupnosti délky n nazveme kvazimediánem, pokud leží v uspořádané posloupnosti na k-tém místě, kde n/10 ≤ k ≤ 9n/10 . Dokažte nebo vyvraťte následující tvrzení:

Kdyby se nám v algoritmu QuickSort podařilo v každém kroku vybrat v čase O(1) jako pivota kvazimedián, algoritmus bude pracovat v nejhorším případě v čase Θ(n log n).

Svoji odpověď zdůvodněte, tj. tvrzení dokažte (pokud platí) či vyvraťte (pokud neplatí).

Poznámka: Ve vaší analýze složitosti můžete předpokládat, že prvky na vstupu jsou po dvou různé.

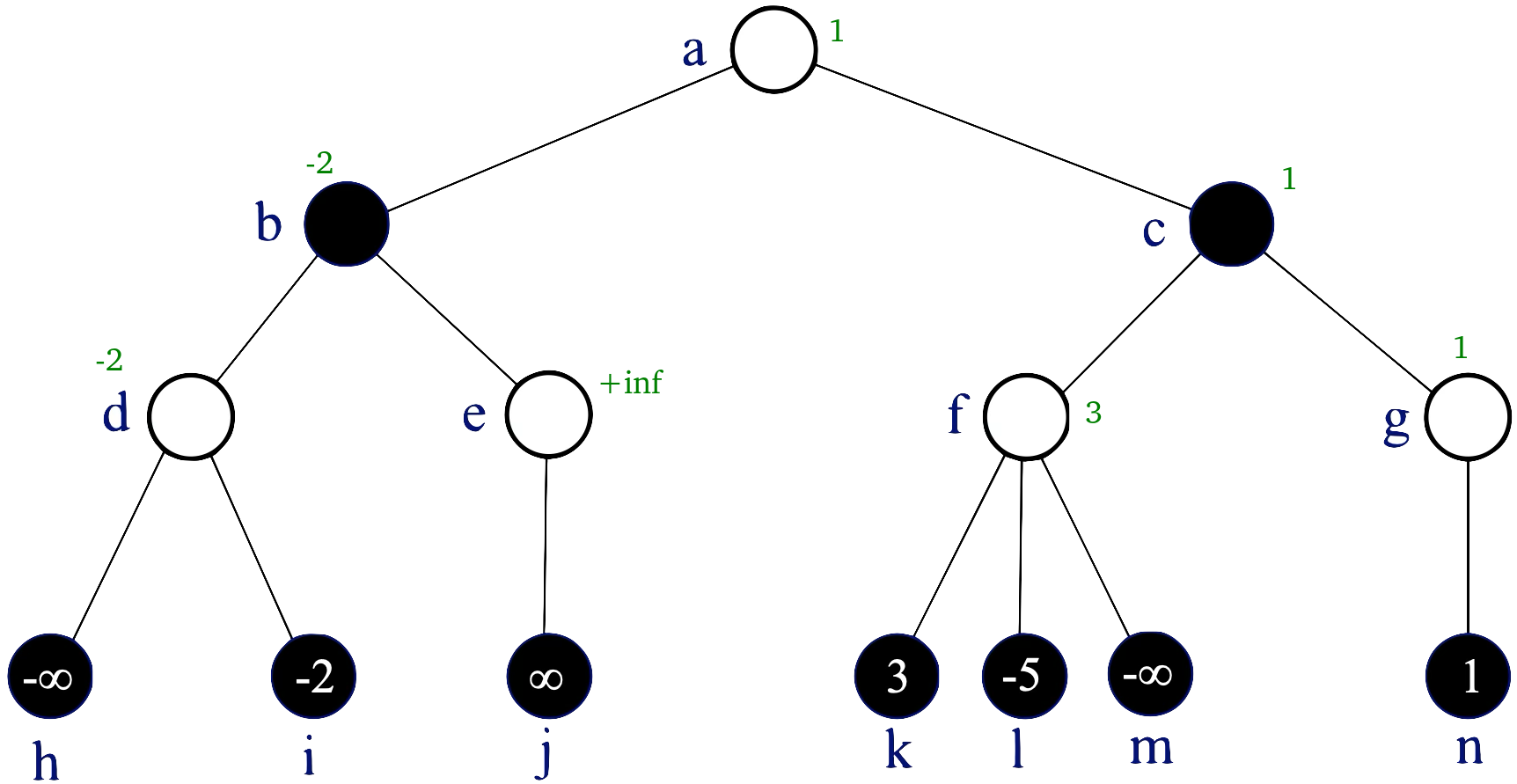
(b) (5 bodů) Strom hry dvou hráčů byl vygenerován do hloubky 3, všechny vrcholy v této hloubce byly ohodnoceny statickou ohodnocovací funkcí a hodnoty zbývajících vrcholů byly spočítány minimaxovým algoritmem. V bílých vrcholech je na tahu hráč maximum, v černých minimum. Výpočet bychom rádi zrychlili metodou alfa-beta prořezávání.

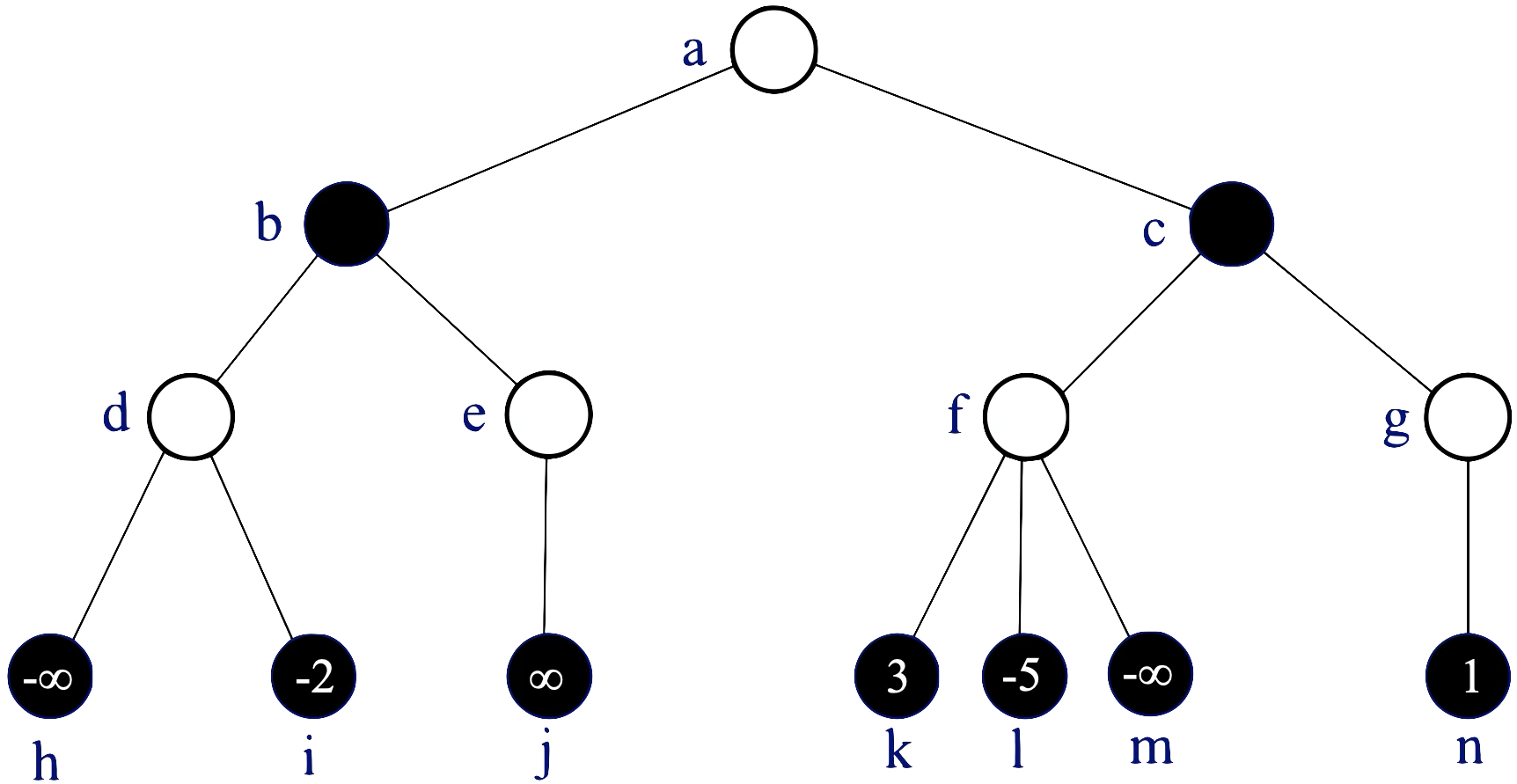
příklad

(b1) Jaká bude minimaxová hodnota kořenu stromu? Stačí uvést hodnotu, nemusíte zdůvodňovat.

Spoiler

Zeleně doplněné hodnoty. V kořeni tedy 1. V bílých vrcholech je na tahu hráč maximum => volím maximum z hodnot dětí. V černých minimum => volím minimum z hodnot dětí. vyplněné hodnoty toho stromu

(b2) V jakém pořadí je třeba procházet strom, abychom se alfa-beta prořezáváním vyhnuli vyhodnocení co nejvíce vrcholů? Pro popis pořadí můžete využít označení vrcholů (a,b,...,n). Kolik vrcholů v takovém případě nemusíme navštívit?

Stačí uvést pořadí vrcholů a počet nenavštívených, nemusíte zdůvodňovat.

(b3) Existuje nějaký průchod stromem, kdy alfa-beta prořezáváním nic neušetříme (tj. pro určení minimaxové hodnoty kořene musíme navštívit a ohodnotit všech 14 vrcholů)? Pokud ano, popište ho, pokud ne, vysvětlete proč.