Zkouška Pangrác 5. 2. 2026

1. 1. Vyslovte princip inkluze a exkluze (formálně např. pomocí sumy, neměla by obsahovat tři tečky)

   2. Máme matici $6\times6$. Kolik existuje daných matic takových, že mají právě 18 jedniček a právě 18 nul?

   3. Máme matici $6\times6$. Kolik existuje daných matic takových, že mají právě 18 jedniček a právě 18 nul a žádná nemá nulový řádek?

2. 1. Definujte řetězec v částečně uspořádané množině $(X,\preceq)$

   Pro $n\in\mathbb{N}$ máme množinu grafů $X_n$ na prvcích $\{1,\ldots,n\}$. Pro jednotlivé grafy platí následující:

   • graf má $i$ vrcholů stupně 0 pro $i\geq0$

   • zbylé $n-i$ vrcholy tvoří cestu

   Zde je příklad platných grafů v $X_5$:

   

   Zde je příklad neplatných grafů v $X_5$:

   

   Částečně uspořádaná množina $(X,\preceq)$ je definovaná následovně: pro každé $M,N\in X_n$ platí $M\preceq N$ právě tehdy, když $M$ je podgrafem $N$.

   1. Uveďte nějaký nejdelší řetězec v $X_n$ (vůči obecnému $n$).

   2. Má částečně uspořádaná množina nějaký největší prvek? Nějaký maximální? Svou odpověď zdůvodněte.

   3. Uveďte nějaký nejdelší antiřetězec (pro obecné $n$). Dokažte, že to je antiřetězec. Nemusíte dokazovat, že je nejdelší.

3. 1. Definujte strom

   2. Pro přirozené $k$ máme strom $T_k$. Pro každé $i$ takové, že $2\leq i\leq k$ platí, že strom má právě jeden vrchol stupně $i$. Strom $T_k$ nemá vrcholy většího stupně než $k$. Zbylé vrcholy jsou listy. Kolik má strom $T_k$ listů (pochopitleně relativně vůči $k$).

4. Vyslovte a dokažte Čebyševovu nerovnost.

5. Pro přirozené $k$ máme graf $Q_k$, jehož $V(Q_n)=\{0, 1\}^k$. To znamená, že každý vrchol sestává z $k$ jedniček a nul. Mezi vrcholy vede hrana právě tehdy, když se liší v právě jedné souřadnici. Toto se nazývá $k$-dimenzionální krychle.

   Příklad $Q_3$:

   

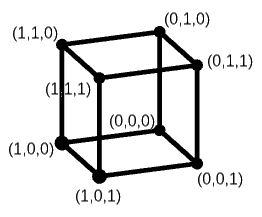
   1. Kolik má $Q_k$ hran (pochopitelně vzato relativně vůči $k$)?

   2. Pro jaké $k$ je $Q_k$ rovinný? Svou odpověď zdůvodněte.