Zkouška Kantor/Pangrác 15. 1. 2026

Chtěl bych upozornit, že toto nejsou přímá znění otázek (jsou spíše hodně zjednodušená). Sepsáno až večer po zkoušce. Čísla v zadání nemusí být ta, která byla ve zkoušce. Byl bych víc než rád, kdyby někdo opravil/dopsal chybějící informace.

Upraveno a doplněno, už by se mělo jednat o přesná znění otázek. :)

Příklad 1

a) [2 body] Definujte, co je to strom.

b) [8 bodů] Když máme graf $G$, jeho průměrný stupeň dostaneme tak, že sečteme stupně všech vrcholů a vydělíme toto číslo počtem vrcholů.

Nyní se omezíme na stromy. Jaký nejmenší průměrný stupeň může mít strom, který má $1000$ vrcholů? Jaký největší? Přiměřeně zdůvodněte své odpovědi.

Příklad 2

a) [2 body] Doplňte následující definici třídy ekvivalence určené prvkem x.

Definice. Nechť X je množina, nechť R je ekvivalence na X a nechť x je prvkem X. Třída ekvivalence určená prvkem x (kterou značíme R[x]) je...

b) [5 bodů] Definujme následující podmnožiny množiny $\mathbb{N}$ (přirozených čísel):

$\bullet$ S je množina všech sudých přirozených čísel,

$\bullet$ P je množina všech prvočísel, a

$\bullet$ L je množina všech složených lichých přirozených čísel.

Existuje nějaká ekvivalence R na N taková, že třídy této ekvivalence jsou přesně množiny S, P, L, t.j. {R[x]; x je prvkem N} = {S,P,L}? Pokud ano, napište, o jakou ekvivalenci se jedná. Pokud ne, nějak přesvědčivě argumentujte, že ne.

(Připomínáme, že $N = \Set{ 1,2,3 \dots }$. Prvočíslo je číslo, které má přesně dva různé dělitele: jedničku a sebe sama. Číslo $1$ tedy není prvočíslo. Složené číslo je číslo, které má alespoň tři různé dělitele: jedničku, sebe sama a nějaké třetí číslo.)

c) [2 body] Nechť X je množina, která má $n$ prvků. Kolik je relací na X? (Pro upřesnění, uvažujeme binární relace.) Proč?

d) [4 body] Kolik je symetrických relací na $n$ prvcích? (Nápověda: jak vypadá maticový zápis symetrické relace?) Proč?

Příklad 3

[4 + 10 bodů] Formulujte a dokažte větu, která nám říká, jaký nejvyšší počet hran může mít rovinný graf na $n$ vrcholech.

Příklad 4

a) [2 body] Nechť X je náhodná veličina na pravděpodobnostním prostoru ($\Omega$, kal.P($\Omega$), P). Napište vzorec pro výpočet střední hodnoty. Můžete si vybrat: buďto ten, který střední hodnotu definuje, nebo praktičtější vzorec, podle kterého se střední hodnota běžně počítá.

b) [5 bodů] Máme zvláštní šestistěnnou kostku: na třech stěnách je napsáno číslo 1, na dvou stěnách číslo 2 a na jedné stěně číslo 3. Hodíme touto kostkou (jen jednou) a označíme X číslo, které nám padlo. X je tedy náhodná veličina. Jakou má X střední hodnotu? Výsledek dostatečně odůvodněte, jen číslo nestačí.

c) [5 bodů] Nyní hodíme touto zvláštní kostkou třicetkrát a označíme Y součet všech hodnot, které nám v těch třiceti hodech padly (tedy Y je náhodná veličina, která nabývá hodnot mezi 30 a 90). Spočítejte střední hodnotu náhodné veličiny Y. Svoje řešení dostatečně odůvodněte.

Příklad 5

Nechť $n$ je přirozené číslo větší než 1. Definujeme graf $G_n$ takto: Jeho vrcholy jsou všechny množiny $A \subset {1, \dots, n}$, pro něž platí $|A| < n$. Dvě z nich jsou spojeny hranou právě tehdy, když jsou disjunktní. Například pro n = 3 dostaneme tento graf:

(obrázek grafu, trochu jako třílistá vrtule v erbu :))

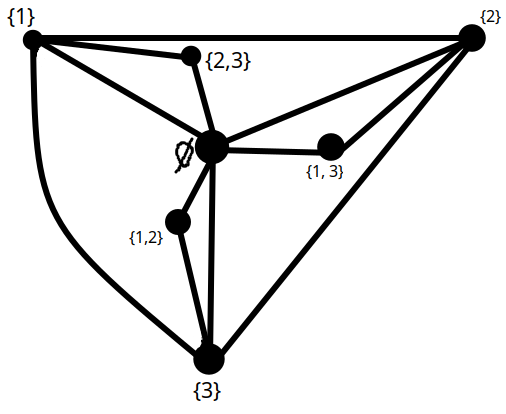
a) [3 body] Pro která n je graf $G_n$ souvislý? Odpověď dostatečně zdůvodněte.

b) [6 bodů] Nechť A $\subset {1, \dots, n}$ je množina velikosti menší než $n$. Jaký je stupeň vrcholu, který odpovídá množině A? (Závisí nějak na velikosti množiny A, na n, nebo případně na něčem jiném?)

c) [2 body] Pro která n je graf $G_n$ eulerovský? Odpověď dostatečně odůvodněte.