1. (10 bodů) Na vstupu je dáno

• vzestupně setříděné pole $a$ celých čísel délky $n$, v němž se čísla mohou libovolně opakovat

• a celá čísla $d$ a $h$ taková, že $d \le h$.

Určete minimální a maximální prvky pole a, které leží v uzavřeném intervalu ‹d,h›. Pokud žádný takový neexistuje, na výstupu bude hodnota None. Pozor na to, že čísla d a h se v poli a vůbec nemusí vyskytovat.

Navrhněte postup, jak správně vyřešit úlohu s co nejlepší časovou a prostorovou složitostí (měřeno nejhorším případem) vzhledem k délce vstupní posloupnosti.

(a) Popište algoritmus (včetně datových struktur, které případně budete používat). Programový kód není povinný, slovní vysvětlení zvoleného postupu řešení naopak povinné je. Nepoužívejte prosím žádné netriviální datové struktury (jako jsou např. datové typy dictionary či set v jazyce Python), jejichž algoritmus sami nepopíšete a neodvodíte jeho časovou složitost.

(b) Zdůvodněte správnost algoritmu.

(c) Odvoďte časovou a prostorovou složitost (v nejhorším případě).

Příklad:

vstup: [-22, -8, -5, 0, 1, 2, 7, 20, 20, 100, 800]
-10 10
výstup: -8 7

vstup: [-22, -8, -5, 0, 1, 2, 7, 20, 20, 100, 800]
50 500
výstup: 100 100

vstup: [-22, -8, -5, 0, 1, 2, 7, 20, 20, 100, 800]
50 90
výstup: None

Poznámka: Za triviální řešení v čase $\Theta(n)$ bude udělen jen velmi nízký počet bodů !

2. (10 bodů) Je zadán strom aritmetického výrazu, tj. binární strom, v jehož vnitřních vrcholech jsou uloženy operátory (+,-,*,/) jako hodnoty typu str a v listech čísla (jako hodnoty typu float). Navrhněte efektivní algoritmus, který vrátí maximální délku podvýrazu, který neobsahuje operátor dělení. Délkou (pod)výrazu rozumíme počet všech operátorů (tj. +,-,*) i operandů (tj. čísel).

Připomeňme, že podvýraz je vždy reprezentován podstromem, který obsahuje všechny následníky svého kořene.

(a) Svoje řešení zapište jako funkci v Pythonu, využijte k tomu definici třídy pro vrchol binárního stromu i hlavičku funkce uvedené níže a váš kód prosím opatřete komentáři,

(b) zdůvodněte správnost,

(c) odvoďte časovou složitost (jako funkci počtu vrcholů n zadaného stromu) metodou nejhoršího případu.

class VrcholBinStromu:

   """třída pro reprezentaci vrcholu binárního stromu"""  
   def  __init__(self, data =  None, levy =  None, pravy =  None):
      self.levy = levy    # levé dítě  
      self.pravy = pravy  # pravé dítě
      self.data = data    # hodnoty (operátory či operandy) uložené ve vrcholech

  

def delka(koren: VrcholBinStromu):

    """
    koren : kořen zadaného binárního stromu
    vrátí : maximální délku podvýrazu bez operátoru dělení
    """

Poznámka: Definici třídy ani hlavičku funkce prosím neměňte, můžete si ovšem definovat vlastní pomocnou funkci (funkce) dle potřeby.

Příklad:

vstup: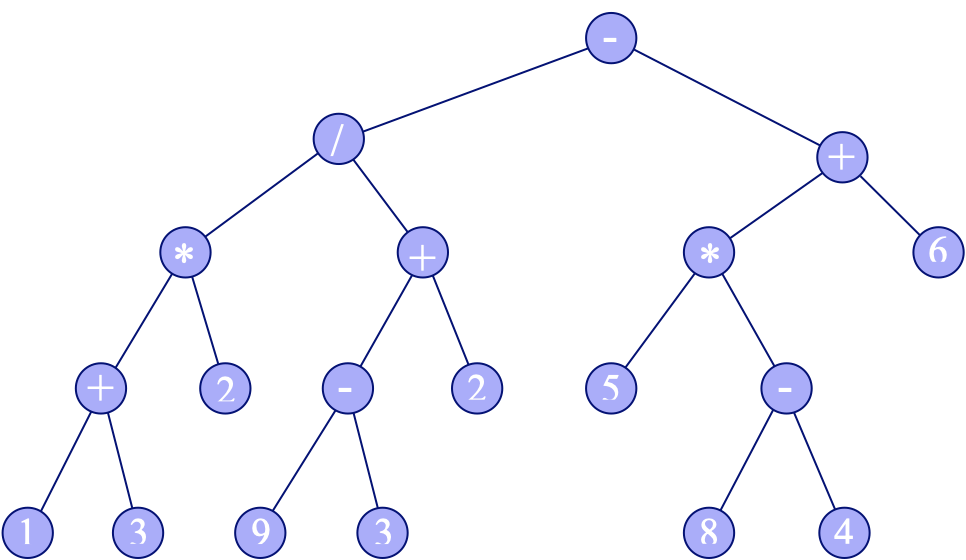
výstup: 7

zdůvodnění: Pravý podstrom kořene neobsahuje operátor dělení a má celkem 7 vrcholů. Naopak žádný podstrom bez operátoru dělení o alespoň 8 vrcholech neexistuje.

3. Odpovězte na otázky, své odpovědi vždy zdůvodněte.

(a) (5 bodů)

(a1) Uspořádejte funkce $n!$, $\ln(n!)$, $2n$, $n \cdot \log n$ do posloupnosti

$f_1$, $f_2$, $f_3$, $f_4$ tak, aby $f_1 = O(f_2)$, $f_2 = O(f_3)$ a $f_3 = O(f_4)$.

(a2) Existují v (a1) dvě různé funkce $f$ a $g$ splňující $f = \Theta(g)$ ? Pokud ano, které to jsou?

Své odpovědi zdůvodněte.

Poznámka:

• $\log n$ označuje $\log_2 n$ (tj. logaritmus při základu dva)

• $\ln n$ označuje $\log_e n$, kde $e$ je Eulerovo číslo s přibližnou hodnotou 2,71828182846

(b) (5 bodů) Uvažme strom hry dvou hráčů max a min, který byl vygenerován do maximální hloubky 30 a jeho listy byly ohodnoceny hodnotami

• $\infty$ (pokud vyhrál max),

• $-\infty$ (vyhrál min) a

• $0$ (nastala remíza).

Protože hloubka stromu hry je > 30, v hloubce právě 30 existují vrcholy, které nejsou listy. Tyto vrcholy byly ohodnoceny statickou ohodnocovací funkcí tak, že pozice výhodnější pro hráče max (min) byly ohodnoceny kladnými (zápornými) čísly. Předpokládejme, že první je na tahu max a po ohodnocení zbylých vrcholů stromu minimaxovým algoritmem byl nakonec kořen ohodnocen hodnotou 0. Profesor Hammerstein se na přednášce otázal studentů, co z toho pro uvedenou hru plyne:

• Bill se domnívá, že v takovém případě nemůže min v žádné partii vyhrát, ať už hraje max jakkoliv;

• Steve soudí, že existuje algoritmus, který pro každý možný tah hráče max poradí hráči min protitah, který zaručí, že pokud hra do nejvýše 30 tahů skončí, min neprohraje;

• Ada si myslí, že existuje algoritmus, který pro každý možný tah hráče min poradí hráči max protitah, který zaručí, že hra skončí neprohrou hráče max (tj. buďto max vyhraje, nebo hra skončí remízou).

Kteří studenti mají pravdu a kteří nikoliv (Bill - ANO / NE, Steve - ANO / NE, Ada - ANO / NE) ? Svoji odpověď zdůvodněte!