Algoritmizace 1 - Zkouška - Töpfer, 13.1.2025

Úloha 1. (10 bodů)

Na vstupu je dán

• vzestupně setříděný (pythonovský) seznam $a$ celých čísel, v němž se čísla mohou libovolně opakovat

• a celá čísla $x$ a $y$ taková, že $x \leq y$

Naším cílem je určit všechny prvky seznamu $a$, které leží v uzavřeném intervalu $\langle x,y\rangle$. Protože seznam je vzestupně setříděný, všechny hledané prvky budou ležet v souvislém úseku, a na výstupu tedy stačí vrátit index prvního a posledního prvku.

Vstup: Vzestupně setříděný (pythonovský) seznam $a$, hodnoty $x$,$y$ takové, že $x \leq y$

Výstup: indexy levy a pravy takové, že $x \leq a[i] \leq y$ právě tehdy, když levy $\leq i \leq$ pravy. None pokud takové indexy neexistují

Navrhněte postup, jak správně vyřešit úlohu s co nejlepší časovou a prostorovou složitostí (měřeno nejhorším případem) vzhledem k délce vstupního seznamu.

(a) Popište algoritmus (včetně datových struktur, které případně budete používat). Programový kód není povinný, slovní vysvětlení zvoleného postupu řešení naopak povinné je. Nepoužívejte prosím žádné netriviální datové struktury (jako jsou např. datové typy dictionary či set v jazyce Python), jejichž algoritmus sami nepopíšete a neodvodíte jeho časovou složitost.

(b) Zdůvodněte správnost algoritmu.

(c) Odvoďte časovou a prostorovou složitost (v nejhorším případě). Do prostorové složitosti počítejte jen paměť, do níž se zapisuje.

Příklady:

vstup:

[-22, -8, -5, 0, 1, 2, 7, 20, 20, 20, 100, 200, 200]
-1 100

výstup: 3 10

vstup:

[-22, -8, -5, 0, 1, 2, 7, 20, 20, 20, 100, 200, 200]
-50 5

výstup:0 5

vstup:

[-22, -8, -5, 0, 1, 2, 7, 20, 20, 20, 100, 200, 200]
333 500

výstup: None

Poznámka: Za triviální řešení v čase $\mathcal{O}(n)$ bude udělen jen nízký počet bodů!

Úloha 2. (10 bodů)

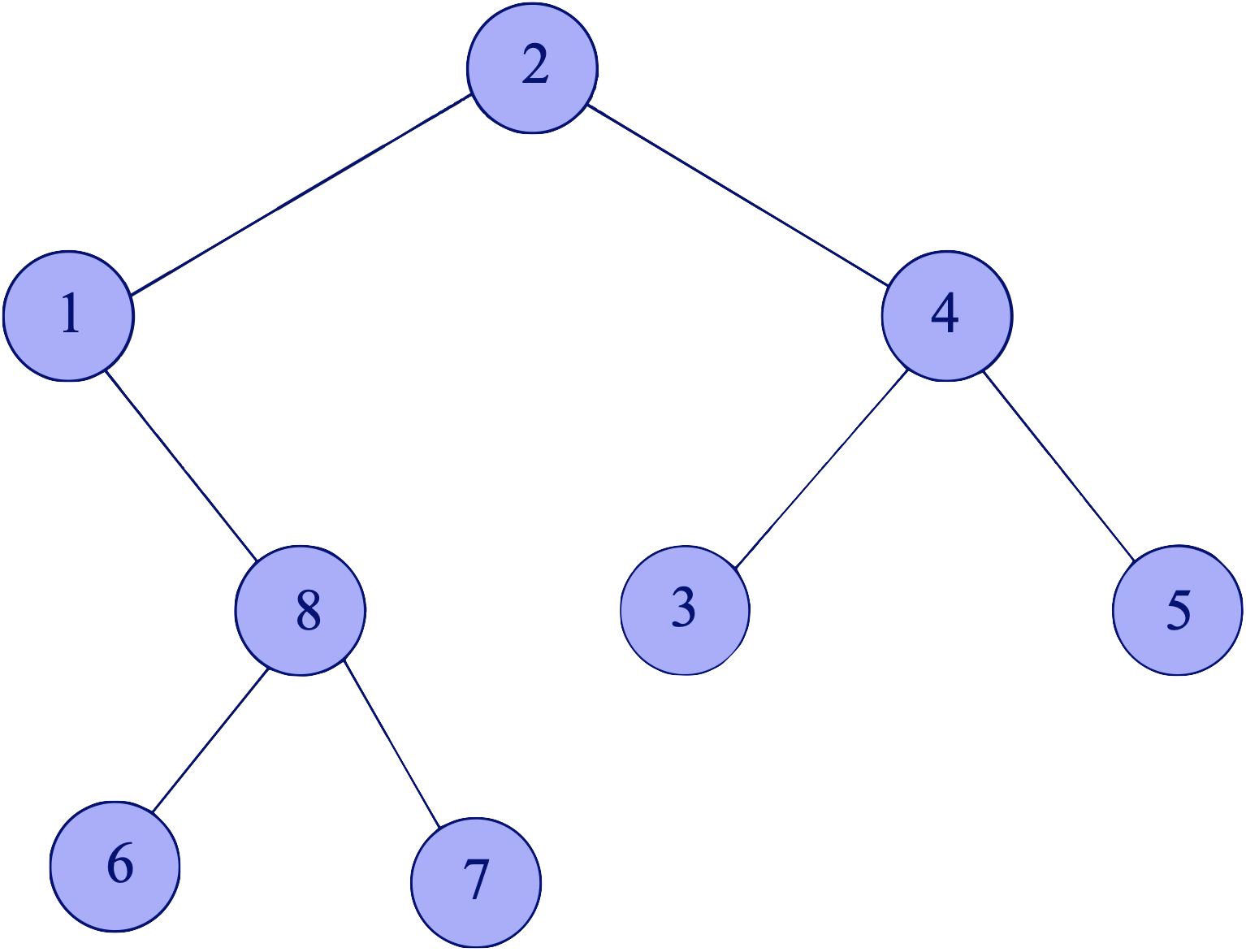
Navrhněte efektivní algoritmus, který pro zadaný binární strom určí jeho nevyváženost, tj. největší celé nezáporné číslo $k$ takové, že existuje vrchol, pro který je absolutní hodnota rozdílu počtu vrcholů v jeho levém a pravém podstromu rovna $k$.

Na obrázku je binární strom o nevyváženosti tři, protože pro vrchol $1$ platí $|0-3|=3$ a neexistuje vrchol, pro nějž by se počty vrcholů v levém a pravém podstromu lišily alespoň o čtyři.

Poznámka: Zajímá nás pouze tvar stromu. Vůbec nehledíme na hodnoty uložené ve vrcholech stromu (atribut data).

(a) Svoje řešení zapište jako funkci v Pythonu, využijte definici třídy pro vrchol binárního stromu i hlavičku funkce uvedené níže a váš kód prosím opatřete komentáři,

(b) zdůvodněte správnost,

(c) odvoďte časovou složitost (v nejhorším případě).

class VrcholBinStromu:
    """třída pro reprezentaci vrcholu binárního stromu""" 
    def __init__(self, data = None, levy = None, pravy = None):
        self.data = data      # data
        self.levy = levy      # levé dítě 
        self.pravy = pravy    # pravé dítě

def nv(koren : VrcholBinStromu):
    """
    koren : kořen binárního stromu
    vrátí : nevyváženost zadaného stromu
    """

Úloha 3. (10 bodů)

Rozhodněte zda platí, své odpovědi vždy zdůvodněte.

(a) (5 bodů) Profesor Hammerstein se na přednášce otázal studentů, co lze říci o časové složitosti následujícího problému:

Vstup: Odkazy na začátky dvou setříděných spojových seznamů, které obsahují celkem n prvků. Můžete předpokládat, že v žádném seznamu se prvky neopakují.

Výstup: Počet prvků takových, že každý se vyskytuje v obou seznamech současně.

• Steve soudí, že v existuje algoritmus, který problém vyřeší v čase $\mathcal{O}(n^2)$

• Bill se domnívá, že časová složitost problému je $\Theta(n \log n)$ (tj. existuje řešení v čase $\mathcal{O}(n \log n)$ a současně každý algoritmus řešení pracuje v čase $\Omega(n \log n)$;

• Ada si myslí, že časová složitost problému je $\Theta(n)$.

Kteří studenti mají pravdu a kteří nikoliv (Steve - ANO / NE, Bill - ANO / NE, Ada - ANO / NE)? Svoji odpověď zdůvodněte!

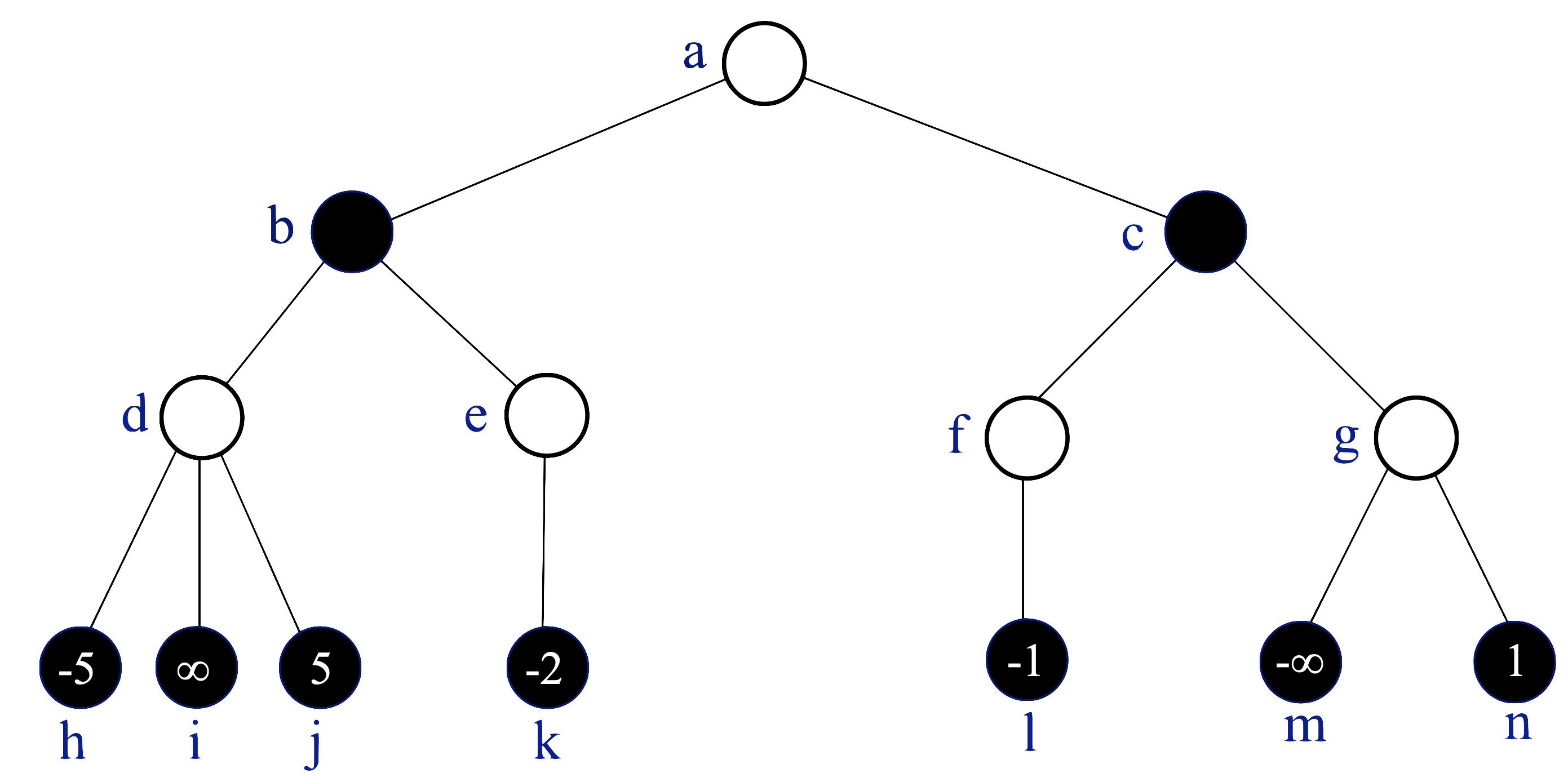
(b) (5 bodů) Strom hry dvou hráčů byl vygenerován do hloubky 3, všechny vrcholy v této hloubce byly ohodnoceny statickou ohodnocovací funkcí a hodnoty zbývajících vrcholů byly spočítány minimaxovým algoritmem. V bílých vrcholech je na tahu hráč maximum, v černých minimum. Výpočet bychom rádi zrychlili metodou alfa-beta prořezávání.

1. Jaká bude minimaxová hodnota kořenu stromu? (odpověď netřeba zdůvodňovat)

2. V jakém pořadí je třeba procházet strom, abychom se alfa-beta prořezáváním vyhnuli vyhodnocení co nejvíce vrcholů? Pro popis pořadí můžete využít označení vrcholů a,b,c,... Stačí uvést pořadí, v němž budou vrcholy navštíveny, netřeba zdůvodňovat.

3. Které vrcholy v takovém případě nemusíme navštívit?

4. Existuje nějaký průchod stromem, kdy alfa-beta prořezáváním nic neušetříme (tj. pro určení minimaxové hodnoty kořene musíme navštívit a ohodnotit všech 14 vrcholů)? Pokud ano, popište ho (použijte označení vrcholů), pokud ne, vysvětlete proč.

Řešení

• předem se omlouvám za gramatické chyby, případně je prosím opravte :)

• pokud si myslíte, že by šlo řešení vylepšit tak se nebojte ho upravit

• bylo ohodnoceno 30/30 a poté upraveno na základě poznámek opravujících

1. Úloha

a)

provedeme binární vyhledávání čísla >= x, když takové najdeme tak si ho zapamatujeme jako "res", pak zkusíme ještě menší dokud nenarazíme na začátek seznamu nebo na číslo které to nesplňuje ("levy" je index posledního čísla co si pamatujeme že to splňuje "res")

• pokud neexistuje číslo >= x vrátíme None, to můžeme implementovat tak že hodnotu poslední hodnoty, která splňovala podmínku "res" nastavíme na None a pokud se nikdy nezmění z None víme že jsme nenašli žádnou hodnotu, která splňuje podmínku

provedeme binární vyhledávání čísla <= y, když takové najdeme tak si ho zapamatujeme jako "res", pak zkusíme ještě větší dokud nenarazíme na konec seznamu nebo na číslo které to nesplňuje ("pravy" je index posledního čísla co si pamatujeme že to splňuje "res")

• pokud neexistuje číslo <= y vrátíme None (implementace viz výše)

tímto vyhledáváním získáme dva indexy, "levy" a "pravy", nebo výsledek None

• může se nám stát že existují čísla která splňují první podmínku (>= x) a i čísla co splňují druhou podmínku (<= y), ale není žádné co splňuje obě dvě (např list [1,4] a x=2, y=3), potom se stane že "levy" > "pravy", v tomto případě také vrátíme None

Implemetace v pythonu:

(dle zadání dobrovolná, ale pokud něco není jasné v textu tak to může kód ujasnit)

def bin_search(l: list, n: int, larger_or_equal: bool=True) -> int|None:
    """
    l = list ve kterém hledáme
    n = porovnávaná hodnota
    larger_or_equal=True hledáme >= n a první výskyt
    larger_or_equal=False hledáme  a poslední výskyt
    
    vrátí index čísla v listu l, který splňuje podmínku, nebo None pokud ji žádný nesplňuje
    """
    left = 0
    right = len(l) - 1
    res = None
    while left <= right:
        mid = (left+right) // 2
        if larger_or_equal: # hledáme >= n
            if l[mid] >= n: 
                res = mid # pamatujeme poslední splňující podmínku
                right = mid - 1 # zkusíme menší (index)
            else:
                left = mid + 1
        else:
            if l[mid] <= n: # hledáme <= n
                res = mid # pamatujeme poslední splňující podmínku
                left = mid + 1 # zkusíme větší (index)
            else:
                right = mid - 1 
    return res

def find_levy_pravy(input_list: list, x: int, y: int) -> tuple[int, int]|None:
    levy = bin_search(input_list, x, larger_or_equal=True)
    if levy is None:
        return None
    pravy = bin_search(input_list, y, larger_or_equal=False)
    if pravy is None:
        return None
    if levy > pravy: # řešíme v textu zmíněnou krajní situaci (např list [1,4] a x=2, y=3)
        return None
    return levy, pravy

if __name__ == "__main__":
    input_list = [0,1,1,1,1,2,3,3,3,4,4]
    x, y = 1, 3
    print(find_levy_pravy(input_list, x, y))

b)

to že je seznam setříděný nám dává najevo že můžeme použít binární vyhledávání

pokud najdeme nejmenší možné číslo, které splňuje >= x a najdeme jeho první výskyt, můžeme si být jistí, že není žádné menší číslo, které by to splňovalo -> index "levy"

• krajní případ, pokud zjistíme, že ani jedno číslo nesplňuje tuto podmínku, vrátíme rovnou None

pokud najdeme největší možné číslo, které splňuje <= y a najdeme jeho poslení výskyt, můžeme si být jistí, že není žádné větší číslo, které by to splňovalo -> index "pravy"

• krajní případ, pokud zjistíme, že ani jedno číslo nesplňuje tuto podmínku, vrátíme rovnou None

proto když vezmeme indexy těchto dvou čísel, tak si můžeme být jistí že splňují:

indexy levy a pravy takové, že x ≤ a[i] ≤ y právě tehdy, když levy ≤ i ≤ pravy

c)

časová: děláme 2 binární vyhledávání -> O(log (N))

prostorová: několik proměnných s konstantní velikostí -> O(1)

2. Úloha

a)

class VrcholBinStromu:
    """třída pro reprezentaci vrcholu binárního stromu""" 
    def __init__(self, data = None, levy = None, pravy = None):
        self.data = data      # data
        self.levy = levy      # levé dítě 
        self.pravy = pravy    # pravé dítě

def nv(koren: VrcholBinStromu):
    """
    koren : kořen binárního stromu
    vrátí : nevyváženost zadaného stromu
    """

    def get_subtree_size_and_balance(vrchol: VrcholBinStromu) -> tuple[int, int]:
        """
        Pro daný vrchol rekurzivně spočítá velikost jeho podstromů a jejich maximální nevyváženost (v kódu "balance")
        
        Vrací 2 čísla:
        počet vrcholů podstromu určeného zadaným vrcholem
        maximalní hodnotu nevyváženosti v podstromu určeného zadaným vrcholem
        """
        # pokud list tak vrátíme počet vrcholů 1 a nevyváženost 0
        if not vrchol.levy and not vrchol.pravy: 
            return 1, 0
        max_balance = 0
        left_size, right_size = 0, 0
        if vrchol.levy: # pokud má levého syna zavoláme rekurzivně na něj
            left_size, max_balance = get_subtree_size_and_balance(vrchol.levy)
        if vrchol.pravy: # obdobně pro pravého
            right_size, right_balance = get_subtree_size_and_balance(vrchol.pravy)
            if max_balance < right_balance: # v max_balance chceme mít max hodnotu, případně ho tedy změníme
                max_balance = right_balance
        current_balance = abs(right_size-left_size) # nalezneme nevyváženost aktuálního podstromu
        if max_balance < current_balance: # v max_balance chceme mít max hodnotu, případně ho tedy změníme
            max_balance = current_balance
        # vrátíme počet vrcholů aktuálního podstromu (počet vrcholů v jeho synech + vrchol)
        # a hodnotu nejvíce nevyváženého vrcholu v aktuálním podstromu
        return right_size+left_size+1, max_balance
    # vrátíme jen maximální nevyváženost, počet vrcholů celého stromu nás nezajímá
    return get_subtree_size_and_balance(koren)[1]

if __name__ == "__main__":
    V = VrcholBinStromu
    koren = V(0, V(0, None, V(0, V(), V())), V(0, V(), V()))
    print(nv(koren))

b)

rekurzivně projdu celý strom, takže si můžu být jistý že žádný vrchol nevynechávám.

• za každý list a každý vrchol přidám k počtu vrcholů jedna -> všechny vrcholy jsou započítány

• v každém vrcholu spočítám nevyváženost a potom vrcholu nad ním předám největší hodnotu nevyváženosti v tomto podstromě

  • což je největší hodnota z těchto: právě spočítaná nevyváženost ve vrcholu, maximální nevyváženost v podstromu daném levým synem, maximální nevyváženost v podstromu daném pravým synem

  • proto si můžu být jistý že když dostanu od syna maximální nevyváženost v jeho podstromu, je to opravdu nevyváženost celého jeho podstromu

-> Proto když se dostanu do kořene můžu si být jistý že maximální hodnota nevyváženosti v celém podstromu určené mým algoritmem odpovídá skutečné maximální nevyváženosti celého stromu

projdu celý strom a každý vrchol navštívím jednou -> algoritmus je konečný

c)

časová: projdu celý strom a každý vrchol navštívím jednou -> O(n) pro strom o n vrcholech

3. Úloha

a)

problém lze řešit následovně:

mějme dva odkazy do seznamů a čítač počtu prvků které jsou v obou

podíváme se na čísla v obou seznamech

• pokud jsou stejná, přičteme 1 z čítači a posuneme oba dva odkazy na odkazy jejich následníky

• pokud je jedno menší než druhé, měníme odkaz na odkaz jeho následníky

opakujeme dokud není aspoň jeden odkaz na konci

při každém porovnání posouváme odkazy minimálně o 1

-> odkazy mohou být posunuty maximálně 2n krát

-> časová složitost O(n)

víme že pokud budeme chtít zjistit které prvky jsou v obou, musíme se na každý prvek aspoň jednou podívat -> Ω(n)

Steve soudí, že v existuje algoritmus, který problém vyřeší v čase O(n2)

ANO - Lze vyřešit v čase O(n2) nebo lepším (v čase O(n)).

Bill se domnívá, že časová složitost problému je Θ(n log n) (tj. existuje řešení v čase O(n log n) a současně každý algoritmus řešení.

NE - To nemůže být pravda protože máme řešení v O(n). A složitost problému Θ(n log n) říká že takové neexistuje.

Ada si myslí, že časová složitost problému je Θ(n).

ANO - Máme řešení v O(n) a víme že to nelze řešit asymptoticky lépe.

b)

Část 1:

Minimaxová hodnota kořenu: -1

Část 2:

V tomto pořadí:

a -> c -> f -> l (l = -1 z toho f = -1)

zpět z c:
g -> n (n = 1 z toho víme že g >= 1, takže si ho MIN nikdy nevybere nad f = -1, z toho c = -1, odřezáváme m)

zpět z a:
b -> e -> k (k = -2 z toho víme že e >= -2, takže b <= -2 a z toho už je jasné že si MAX nikdy nevybere <= -2 nad -1, z toho b = -2, odřezáváme d, h, i, j) 

Část 3:

Nemusíme navštívit: d, h, i, j, m

Část 4:

Ano existuje:

a -> b -> d -> h
-> j
-> i

zpět z b:
e -> k

zpět z a:
c -> g -> m
-> n

zpět z c:
f -> l